Se o caixeiro tivesse que passar por apenas 3 cidades, digamos, Rio de Janeiro, São Paulo e Curitiba, teria 6 possíveis ordenações para percorrê-las:

Rio – São Paulo – Curitiba
Rio – Curitiba – São Paulo
São Paulo – Rio – Curitiba
São Paulo – Curitiba – Rio
Curitiba – Rio – São Paulo
Curitiba – São Paulo – Rio

Como calculamos o número de ordenações? Veja: temos 3 opções para a primeira cidade: Rio, São Paulo ou Curitiba. Quando escolhemos a primeira cidade, ficamos com duas opções para escolher a segunda cidade, então são 3 × 2 = 6 maneiras de fixar qual serão a primeira e a segunda cidades. Claro que, uma vez que a primeira e a segunda estejam fixadas, não nos resta opção para a última. Então são 6 possíveis ordenações.

O número total de ordenações possíveis de N elementos é chamado de permutação de N elementos.

Mas e com as 26 capitais? Temos 26 opções para a primeira cidade. Para cada escolha de primeira cidade, ficamos com 25 opções de segunda cidade, logo são 26 vezes 25 formas de decidir quais serão as duas primeiras cidades. Para cada opção que fizermos com relação às duas primeiras cidades, ficaremos com 24 possibilidades para a terceira cidade. Logo há 26 × 25 × 24 formas de quais serão a primeira, a segunda e a terceira cidade. Seguindo esse raciocínio, vemos que o número total de formas de ordenar as 26 cidades é:

26 × 25 × 24 × 23 × 22 × 21 × ... × 5 × 4 × 3 × 2 × 1.

Para denotar mais facilmente produtos deste tipo, isto é, o produto de todos os números naturais de 1 até um certo número N utilizamos o símbolo N! e lemos N fatorial. Assim, temos 26! possíveis ordenações das 26 capitais.

A chamada de áudio nos conta que se levássemos apenas um segundo para calcular a distância total de cada percurso, gastaríamos cerca de um bilhão de vezes a idade do universo para terminar as contas. Vamos verificar essa informação?

Estima-se que o universo tem aproximadamente 13,7 bilhões de anos, isto é, 13.000.000.000 de anos.

Quantos segundos gastaríamos para fazer as contas das distâncias de todos os percursos possíveis do caixeiro para visitar as 26 capitais? Se são 26! percursos possíveis e gasta-se um segundo para cada percurso, gastaríamos 26! segundos. Mas quanto é 26 fatorial? Se você tiver uma calculadora científica, pode digitar 26 e depois calcar no ponto de exclamação e obterá o resultado. Se não tem calculadora científica, o jeito é fazer as multiplicações uma a uma: 26 × 25 × 24 × 23 × ... × 3 × 2 × 1.

De qualquer forma que você faça, vai descobrir que

26! = 403.291.461.126.605.635.584.000.000.

Isso quer dizer que gastaríamos 403.291.461.126.605.635.584.000.000 segundos para calcular as distâncias de todos os percursos. Como cada hora tem 60 minutos e cada minuto tem 60 segundos, resulta que cada hora tem 3.600 segundos. Logo, dividindo por 3.600, descobrimos que gastaremos

112.025.405.868.501.565.440.000 horas

para fazer todos os cálculos. Observando que cada dia tem 24 horas, isso equivale a

4.667.725.244.520.898.560.000 dias.

Como cada ano tem 365 dias, podemos calcular quantos anos levaremos dividindo por 365. Obtemos

12.788.288.341.153.146.739 anos (e mais alguns dias)

Como o universo tem aproximadamente 13 bilhões de anos, vamos dividir por 13 bilhões. Obtemos, arredondando, que

12.788.288.341.153.146.739 anos = 983.714.487 vezes a idade do universo.

Mas isso é praticamente um bilhão de vezes a idade do universo!!!

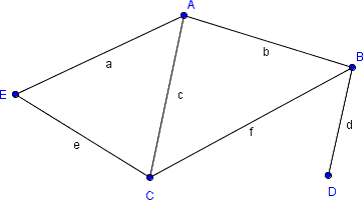
O problema do caixeiro viajante é uma importante questão da área de otimização matemática. Tem grande relevância para o campo da logística e da produção, além de outros.

A modelagem matemática do problema é feita através de uma estrutura matemática denominada grafo. Um grafo é um conjunto de pontos (que chamamos de vértices), os quais podem ser associados através de linhas (que chamamos de arestas). Na figura a seguir temos um grafo com 5 vértices e 6 arestas.

No grafo associado ao problema do caixeiro viajante, cada cidade é representada por um vértice, e as arestas representam as vias (estradas, por exemplo) que ligam as cidades. A cada aresta podemos associar um número que representa a distância entre as duas cidades conectadas por ela.

O obstáculo à resolução deste problema, como vimos, é o crescimento exponencial do número de trajetos quando aumenta-se o número de cidades. Esta característica torna inviável o uso da comparação de todas as trajetórias como forma de decidir qual a ótima. Em vez disso, pesquisadores buscam métodos alternativos que sejam viáveis computacionalmente e que gerem soluções próximas da solução ótima.

Para saber mais sobre crescimento exponencial, acesse: http://www.uff.br/cdme/exponencial/.

Devlin, K. Os Problemas do Milênio – Sete Grandes Enigmas Matemáticos de Nosso Tempo. Editora Record, 2004.