Cálculo Diferencial de Várias Variáveis
Versão 2002.1

Este livro nasceu das notas de aula do curso de Cálculo Diferencial de Funções de Várias Variáveis para os alunos de Economia, Engenharia, Física, Química e Matemática, da PUC-Rio. A proposta é o de apresentar os conceitos e técnicas de Cálculo Diferencial, usando problemas de otimização como um forte elemento motivador. Esta diretiva é empregada em todo o livro. Nossa experiência, ao longo de quase cinco anos, tem mostrado um resultado muito positivo com este tipo de procedimento.

Logo no primeiro exemplo do primeiro capítulo (o problema da caixa), o aluno recorda como a derivada é uma ferramenta extremamente poderosa para resolver um problema de otimização, no caso, um problema de otimização unidimensional. Nos dois exemplos seguintes, o aluno é desafiado a tentar resolver dois problemas de otimização multidimensionais: o problema da dieta e o problema do planejamento hidrotérmico. O aluno convence-se, então, da dificuldade de resolver tais problemas e da necessidade de ferramentas matemáticas adequadas para fazê-lo.

Mas mais do que uma finalidade, a linguagem de otimização é extremamente adequada para introduzir alguns dos objetos fundamentais de Cálculo Diferencial a Várias Variáveis: as derivadas parciais, as derivadas direcionais e o vetor gradiente. Em geral, ao motivar estes conceitos pela primeira vez no livro, deu-se preferência a um contexto econômico (lucro, custo), no lugar de um contexto físico (posição, velocidade). Nossa experiência mostra que os alunos sentem-se mais confortáveis num contexto econômico (o artigo de Crowe e Zand apresenta um exemplo muito interessante que ilustra este ponto de vista). Naturalmente, as aplicações em Física não foram esquecidas e estão presentes no livro.

O texto é escrito em estilo coloquial e, apesar de quase 600 páginas, é muito fácil de se ler. Um cuidado especial foi tomado com a elaboração das mais de 250 figuras que aparecem no texto.

Existem algumas diferenças no texto, com relação ao enfoque que se dá tradicionalmente nos livros de Cálculo Diferencial a Várias Variáveis, que gostaríamos de comentar.

1. A linguagem matricial é amplamente usada no texto. Afinal, um dos resultados fundamentais na teoria de Cálculo Diferencial é que, sob certas condições, uma função "complicada" pode ser aproximada por uma função muito mais simples na vizinhança de um ponto, a saber, uma transformação linear. Mais ainda: a partir do estudo das propriedades desta transformação linear (algo supostamente mais fácil de fazer), consegue-se estabelecer propriedades (locais) de interesse da função original. O método de Newton é um exemplo formidável desta idéia. Outro benefício: com o uso de matrizes, a regra da cadeia fica mais fácil de ser entendida e aplicada. Caso necessário, o aluno consegue deduzir facilmente qualquer "regra da cadeia em termos das funções coordenadas", a partir da versão matricial. Um curso de Álgebra Linear, embora recomendado, não é pré-requisito para o uso deste livro. As noções básicas de Álgebra Linear são introduzidas no texto, incluindo a definição de transformação linear e sua representação matricial.

2. A classificação local de pontos críticos é feita para o caso geral, e não somente para funções que dependam de duas ou três variáveis. No texto, apresentamos três métodos que permitem classificar a positividade da matriz hessiana da função em um ponto crítico: o método de Lagrange (completamento de quadrados), menores principais e autovalores.

3. Teoremas que garantem a globalidade de um ponto crítico são apresentados. Para isto, introduzimos as definições e propriedades básicas de conjuntos convexos, funções côncavas e convexas. Em particular, apresentamos dois exemplos interessantes que mostram como certos resultados que são verdadeiros no caso unidimensional, tornam-se falsos quando adaptados para o caso multidimensional.

4. O teorema dos multiplicadores de Lagrange é estudado no caso geral, isto é, com um número arbitrário de restrições em igualdade.

5. No caso do conjunto admissível ser construído com restrições em desigualdade (ou mesmo com restrições mistas), o que se sugere é procurar por candidatos no interior do conjunto admissível (pontos críticos da função-objetivo) e, em seguida, com o teorema dos multiplicadores de Lagrange, procurar por candidatos na fronteira do conjunto admissível, analisando os vários casos possíveis (isto é, candidatos em faces, arestas ou vértices). No livro, apresentamos um resultado que unifica este tratamento: o teorema de Karush-Kuhn-Tucker. Publicado em 1950, este teorema iniciou a teoria moderna de otimização não-linear. Tanto em aspectos teóricos quanto computacionais, o teorema possui várias aplicações em Economia, Engenharia e Matemática

O material deste livro pode ser perfeitamente coberto em um curso semestral, com 4 horas por semana. O texto segue uma ordem canônica, mas pode haver alterações, sem prejuízo para o curso. Por exemplo, o teorema de Weierstrass, tratado no capítulo 4, pode ser visto antes do capítulo 11 (otimização com restrições). Outra prática é a de se apresentar uma versão preliminar da regra da cadeia para o caso de composições de funções escalares com curvas parametrizadas, seguir com o capítulo 8 sobre derivadas direcionais e o vetor gradiente e, depois, voltar para o capítulo 7, para estudar a versão geral da regra da cadeia. Boa parte do conteúdo do capítulo 2 pode ser omitida, pois o aluno já estudou vetores em um curso de Física no Ensino Médio e, provavelmente, também já o fez em um curso preliminar de Álgebra Linear no Ensino Superior. As seções com um asterisco (*) apresentam assuntos avançados, e podem ser omitidas em uma primeira leitura.

Os exercícios são apresentados no final de cada capítulo e, embora não haja uma indicação explícita, eles são divididos de acordo com cada seção. Os exercícios são apresentados quase sempre em ordem crescente de dificuldade. Um asterisco (*) indica explicitamente um exercício mais elaborado ou um exercício com conteúdo opcional. No apêndice C, colocamos as respostas de alguns exercícios. Mas, mais do que obter a resposta final, o aluno deve ter consciência da importância de escrever uma justificativa coerente, que o conduza à resposta. Isto é especialmente verdade para os exercícios do tipo "verdadeiro ou falso".

Não colocamos as respostas dos exercícios que pedem o cálculo explícito de derivadas parciais, matrizes jacobianas e hessianas no apêndice C. O aluno pode usar um sistema de computação simbólica para verificar suas respostas. No apêndice A, descrevemos os comandos básicos do MuPAD Light (um sistema de computação simbólico gratuito para professores e alunos) que permitem fazer estas contas. No apêndice B, descrevemos os comandos básicos análogos para o software MapleV.

O endereço na internet para a página web do livro é:

http://www.mat.puc-rio.br/~hjbortol/cdfvv/livro/

Nesta página, você encontrará uma coleção de links interessantes para um curso de Cálculo Diferencial de Funções de Várias Variáveis, o que inclui fatos históricos, as biografias dos vários matemáticos que desenvolveram os teoremas que aparecem no texto, entrevistas, aplicações da teoria de otimização, grupos de discussão, programas de computador e, naturalmente, a errata do livro. O símbolo

nas margens direita ou esquerda de uma página, indica explicitamente a existência de um link para o exemplo ou exercício resolvido em questão. Em particular, um applet JAVA foi especialmente desenvolvido, com o objetivo de permitir a visualização tridimensional de gráficos de funções de duas variáveis e superfícies de nível de funções de três variáveis, que aparecem no texto. Por exemplo, a figura abaixo

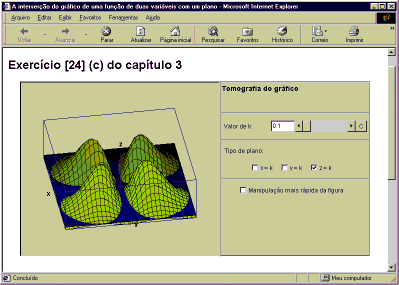
mostra o uso deste applet para visualizar o gráfico da função do item (c) do exercício [24] do capítulo 3,

z = f(x, y) = 15(x²y²e^(-x2-y2))/(x²+y²)

definida no quadrado [-2, +2] x [-2, +2]. Com o applet, ainda é possível girar, encolher ou ampliar o desenho. O uso do applet é particularmente útil nos capítulos iniciais, onde tentamos criar uma percepção geométrica tridimensional. Para usar os applets, seu navegador deverá estar com a opção "JAVA" habilitada. Além dos exemplos disponíveis, você poderá adaptar estes applets para visualizar suas próprias funções! Acesse a página web do livro para obter instruções detalhadas de como fazê-lo.

Um outro recurso computacional interessante é o programa MuPAD, um ambiente desenvolvido para cálculos matemáticos, sejam eles simbólicos, numéricos ou gráficos. Com ele você poderá obter soluções exatas de muitos problemas matemáticos, incluindo fatoração de números inteiros e polinômios, cálculo com matrizes, sistemas lineares e não-lineares de equações, números complexos, trigonometria, limites, derivadas, integrais, equações diferenciais, etc. O programa é desenvolvido por um grupo de pesquisadores da Universidade de Paderborn, Alemanha. Sua distribuição é gratuita para professores e alunos. Você poderá obter uma cópia do MuPAD no endereço

http://www.sciface.com/mupad_download/

através de um registro gratuito. Versões para outros sistemas operacionais (Linux, Macintosh, Solaris) podem ser obtidas no mesmo endereço. No apêndice A, você encontrará um tutorial com os comandos básicos do MuPAD, relevantes para um curso de Cálculo Diferencial de Funções de Várias Variáveis.

Este livro foi produzido inteiramente em LaTeX2e, usando o ambiente MiKTeX de Christian Schenk. Parte do texto (cerca de 80%) foi digitada usando o editor VIM, de Bram Moolenaar e a outra parte digitada com o uso do editor WinEdt, de Aleksander Simonic.

Todas as figuras foram geradas por computador. A partir das equações, o programa Maple V foi utilizado para produzir a figura em um arquivo postscript para, então, ser convertido para o formato encapsulated postscript, com os programas Ghostscript e GSview. Isto produzia um primeiro esboço. Retoques finais (texto, setas, padrões de preenchimento, espessura das linhas. etc.) foram efetuados com o programa Adobe Illustrator, para produzir a versão final da figura.

A definição do formato da Terra não envolve a descrição de montanhas e vales mas, sim, o formato da superfície do nível do mar e sua continuação hipotética sobre as porções de terra, eliminando-se os efeitos das ondas, ventos, correntes e marés. Esta superfície é denominada geóide.

Pode-se mostrar que o geóide é uma superfície de nível do potencial gerado pelo campo gravitacional da Terra. Sendo assim, em cada ponto do geóide, a linha de prumo é sempre perpendicular ao geóide. Esta propriedade faz do geóide uma referência natural para medir alturas.

Por causa das distribuições irregulares de massa na Terra e de anomalias gravitacionais, a descrição matemática do geóide não é muito simples e, por este motivo, formas geométricas mais elementares foram sugeridas para se aproximar o geóide, como a esfera e o elipsóide de revolução.

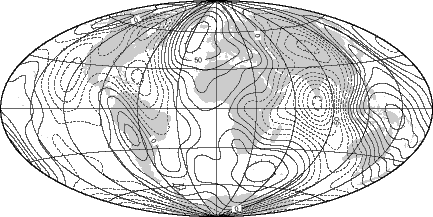
A figura da capa, produzida pelo programa de computador GMT (de Wessel e Smith), mostra a projeção de Hammer das curvas de nível da altura do geóide com relação a um elipsóide de referência. Níveis positivos são desenhados com uma linha sólida e níveis negativos com uma linha tracejada.

Antes de tudo, gostaria de agradecer a Geovan Tavares dos Santos, coordenador do projeto MatMídia. Sem seu empenho, dedicação, entusiasmo e pioneirismo, este livro não teria sido publicado.

Gostaria de agradecer também às várias pessoas que colaboraram com sugestões e correções durante o processo de elaboração deste livro. Entre elas: Ana Tereza Figuereido Vasconcellos, Márcio Henrique Gonçalves Pinto, Mariana Martins, Constanza Cortes, Filipe Colaço, Bernardo Schneider, Raphaela Pimentel de Azevedo Athayde, Glenda Bezerra Lustosa, Roberta Levy Martins, Daniel Chrity, Mário Maia Nevares, Eduardo Marques, Vanessa Baldi, Carolina Damazio, Luis Eduardo Ávila de Souza, José Américo Rodrigues Araújo Filho, Rafael Ruggiero Rodriguez e Sérgio Bernardo Volchan. Em especial, gostaria de agradecer a Francisco Satuf Rezende, Luciana Arruda, Moema Ribeiro da Silva e Ricardo Soares Leite, pela leitura e crítica minuciosas do texto.

Finalmente, gostaria de agradecer a Marco Antônio Grivet Mattoso Maia e Walter H. F. Smith, por permitirem a reprodução dos mapas no livro; e a Konrad Polthier e Letícia Gentile Veiga, pela ajuda na programação dos applets JAVA disponíveis na página web do livro.